Next: Considerations regarding the selection of the parameter r Up: Generalized Multiscale Entropy (GMSE) Analysis: Quantifying the Structure Previous: Generalized Multiscale Entropy (GMSE) Analysis: Quantifying the Structure
The original multiscale entropy (MSE) method [1,2] quantifies the complexity of the temporal changes in one specific feature of a time series: the local mean values of the fluctuations. The method comprises two steps: 1) coarse-graining of the original time series, and 2) quantification of the degree of irregularity of the coarse-grained (C-G) time series using an entropy measure such as sample entropy (SampEn) [3].
The generalized multiscale entropy (GMSE) method [4] quantifies the complexity of the dynamics of a set of features of the time series related to local sample moments. The method differs from the original MSE in the way that the C-G time series are computed. In the original method, the mean value is used to derive a set of representations of the original signal at different levels of resolution. This choice implies that information encoded in features related to higher moments is discarded. The coarse-graining procedure in the generalized algorithm extracts statistical features such as the variance (standard deviation [SD] or mean absolute deviation [MAD]), skewness, kurtosis, etc, over a range of time scales. This tutorial focuses primarily on the quantification of the information encoded in fluctuations in standard deviation.
We use a subscript after MSE to designate the type of coarse-graining employed. Specifically, MSEμ, MSEσ and MSEσ2 refer to MSE computed for mean, SD and variance C-G time series, respectively.
For a dynamical property of interest, such as mean or standard deviation, MSE algorithms comprise two sequential procedures:
As noted above, in the original MSE method (MSEμ) the property of interest is the local mean value. The C-G time series capture fluctuations in local mean value for pre-selected time scales. In the original application, such C-G time series were obtained by dividing the original time series into non-overlapping segments of equal length and calculating the mean value of each of them. However, other approaches for extracting the same “type” of information (local mean) can also be considered, including low pass filtering the original time series using Fourier analysis, among others (e.g., the empirical mode decomposition) methods.
The GMSE method expands the original MSE framework to other properties of a signal. Here, we address the quantification of information encoded in the fluctuations of the “volatility” of the signal.
Figure 1 shows the interbeat interval (RR) time series from a healthy subject, simulated 1/f noise and their SD C-G time series for scales 5 and 20. The fluctuation patterns of the physiologic C-G time series appear more unpredictable, “less uniform” and more “bursty,” than those of simulated 1/f noise.
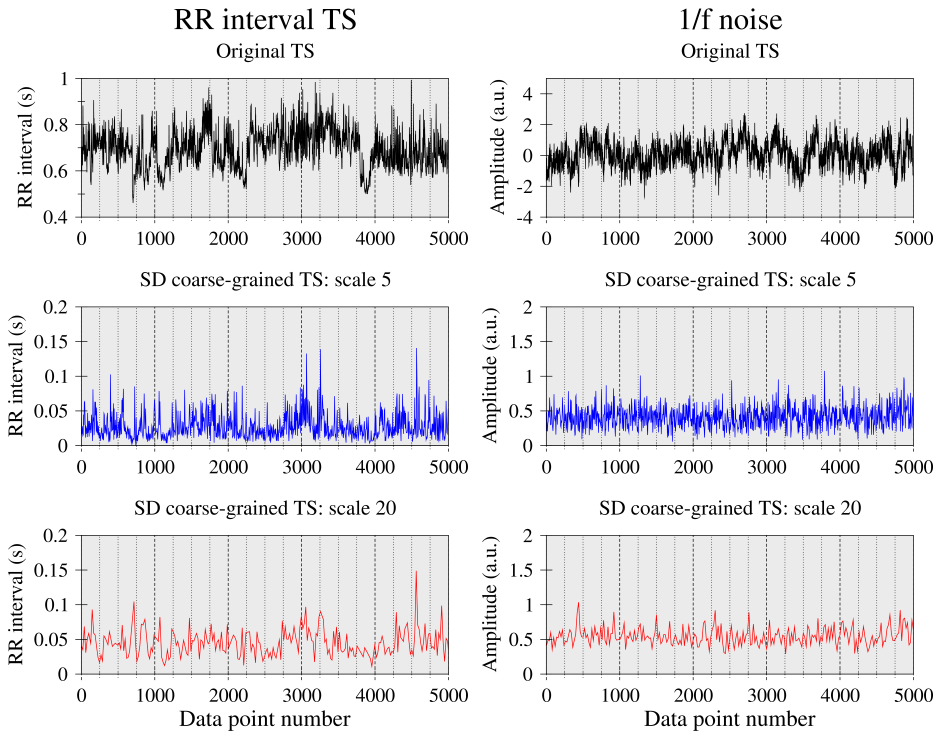
|
Figure 2 shows MSEσ (top panels) and MSEσ2 (bottom panels) analyses of physiologic and simulated long-range correlated (1/f) noise time series. The physiologic time series are the RR intervals (left panels) from healthy young to middle-aged (≤ 50 years) and healthy older (> 50 years) subjects and patients with chronic (congestive) heart failure (CHF). The time series are available on PhysioNet: i) 26 healthy young subjects and 46 healthy older subjects (nsrdb, nsr2db) ii) 32 patients with CHF class III and IV (chfdb, chf2db).
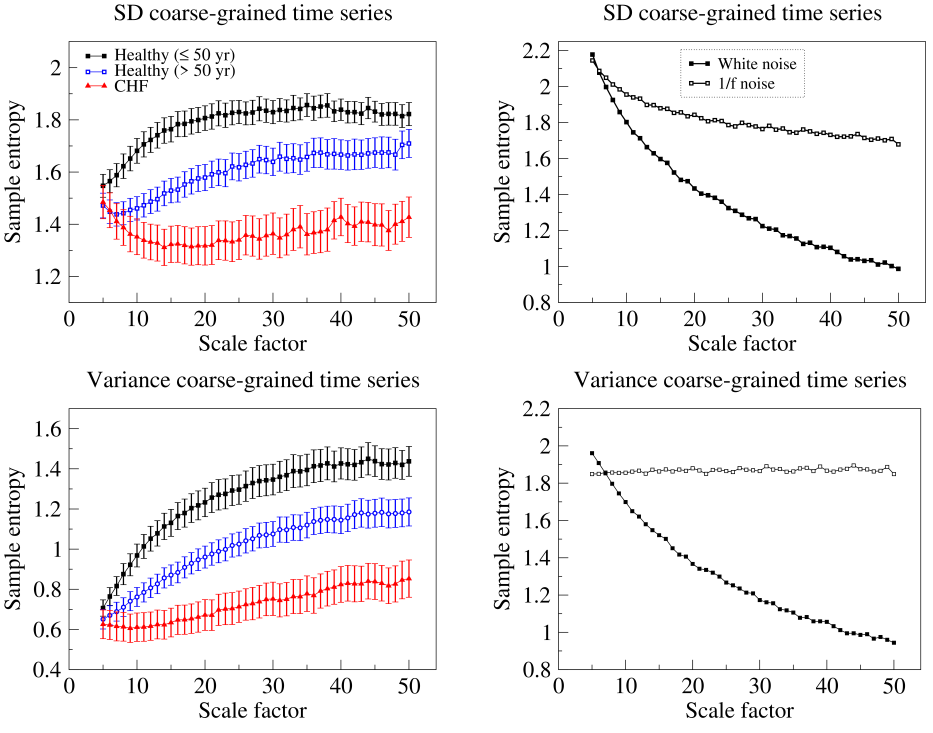
|
Entropy over the pre-selected range of scales was higher for 1/f than white noise, both for SD and variance C-G time series. With respect to the RR interval time series, entropy values were on average higher for the group of healthy young subjects than for the group of healthy older subjects. In addition, the entropy values for the group of CHF patients were, on average, the lowest. The results were qualitatively the same for SD and variance C-G time series.
These findings are consistent with those derived from traditional (mean C-G) MSE analyses. They indicate that: 1) 1/f noise processes are more complex than uncorrelated random ones; 2) the complexity of heart rate dynamics degrades with aging and heart disease.
Madalena Costa (mcosta3@bidmc.harvard.edu)